 /
/ 
Time Limit: 4 sec / Memory Limit: 256 MB
配点 : 900 点
問題文
シカのAtCoDeerくんは正方形のタイルを N 枚持っています。 各正方形の片面には 1~N の数が書いてあって、正方形の各頂点にはそれぞれ色が塗られています。色は 0~999の整数で表され、 i と書かれた正方形に塗られている色は、数の書かれている方向から見て左上、右上、右下、左下 の順に、 C_{i,0},C_{i,1},C_{i,2},C_{i,3} で与えられます(図1を参照)。
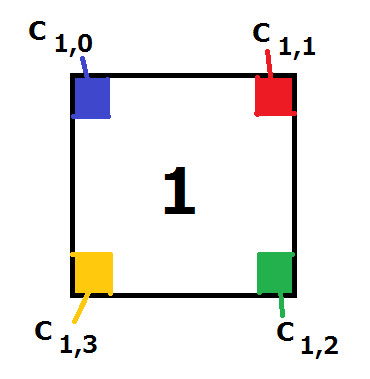
図1: タイルの色と入力の対応
AtCoDeerくんはこれらのタイルを6枚組み合わせて次のような条件を満たす立方体を作ろうと考えました。
- 数の書いてある面が外側を向いている
- 立方体の各頂点に対し、そこに集まる正方形の頂点は3つあるが、それらには全て同じ色が塗られている
AtCoDeerくんのために条件を満たす立方体が何通りあるか求めてください。ただし、正方形には数が書いてあるので、色の構成が同じだとしても使ったタイルが異なったり、使ったタイルの向き(90°回転により4通り考えられる)が異なるものは異なる立方体とみなします。 ただし、3次元空間で回転させることで使ったタイルの向きまで完全に一致するものは同じ立方体とみなします。
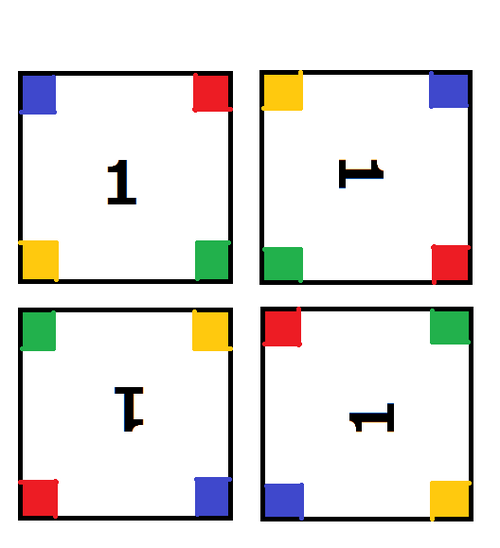
図2: 4方向のタイルの向き
制約
- 6≦N≦400
- 0≦C_{i,j}≦999 (1≦i≦N , 0≦j≦3)
入力
入力は以下の形式で標準入力から与えられる。
N
C_{1,0} C_{1,1} C_{1,2} C_{1,3}
C_{2,0} C_{2,1} C_{2,2} C_{2,3}
:
C_{N,0} C_{N,1} C_{N,2} C_{N,3}
出力
AtCoDeerくんが作れる立方体が何通りあるか出力せよ。
入力例 1
6 0 1 2 3 0 4 6 1 1 6 7 2 2 7 5 3 6 4 5 7 4 0 3 5
出力例 1
1
下図のような立方体が作れます。
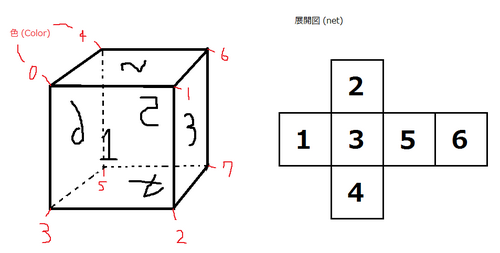
入力例 2
8 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1
出力例 2
144
入力例 3
6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
出力例 3
122880
Score : 900 points
Problem Statement
AtCoDeer the deer has N square tiles. The tiles are numbered 1 through N, and the number given to each tile is written on one side of the tile. Also, each corner of each tile is painted in one of the 1000 colors, which are represented by the integers 0 between 999. The top-left, top-right, bottom-right and bottom-left corner of the tile with the number i are painted in color C_{i,0}, C_{i,1}, C_{i,2} and C_{i,3}, respectively, when seen in the direction of the number written on the tile (See Figure 1).

Figure 1: The correspondence between the colors of a tile and the input
AtCoDeer is constructing a cube using six of these tiles, under the following conditions:
- For each tile, the side with the number must face outward.
- For each vertex of the cube, the three corners of the tiles that forms it must all be painted in the same color.
Help him by finding the number of the different cubes that can be constructed under the conditions. Since each tile has a number written on it, two cubes are considered different if the set of the used tiles are different, or the tiles are used in different directions, even if the formation of the colors are the same. (Each tile can be used in one of the four directions, obtained by 90° rotations.) Two cubes are considered the same only if rotating one in the three dimensional space can obtain an exact copy of the other, including the directions of the tiles.

Figure 2: The four directions of a tile
Constraints
- 6≦N≦400
- 0≦C_{i,j}≦999 (1≦i≦N , 0≦j≦3)
Input
The input is given from Standard Input in the following format:
N
C_{1,0} C_{1,1} C_{1,2} C_{1,3}
C_{2,0} C_{2,1} C_{2,2} C_{2,3}
:
C_{N,0} C_{N,1} C_{N,2} C_{N,3}
Output
Print the number of the different cubes that can be constructed under the conditions.
Sample Input 1
6 0 1 2 3 0 4 6 1 1 6 7 2 2 7 5 3 6 4 5 7 4 0 3 5
Sample Output 1
1
The cube below can be constructed.

Sample Input 2
8 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1
Sample Output 2
144
Sample Input 3
6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Sample Output 3
122880