 /
/ 
Time Limit: 2 sec / Memory Limit: 512 MB
配点 : 1300 点
問題文
シカのAtCoDeerくんはある日、 N 頂点 M 辺からなる単純な(すなわち、多重辺と自己ループのない)グラフを拾いました。頂点には1,2,..,Nの番号がついていて互いに区別が可能で、辺は(a_i,b_i) (1≦i≦M)で表されます。 AtCoDeerくんは K 色のペンキを使って各辺を塗ろうとしています。ペンキは大量にあるので同じ色で複数の辺を塗ることが可能です。 AtCoDeerくんの拾ったグラフは特殊な形状をしているため、単純なサイクル(すなわち,サイクルであって同じ頂点を一度しか通らないもの)を選んで、そのサイクル上の辺の色をひとつずつサイクルに沿ってずらすことが出来ます。正確に言うと、サイクル上の辺を順に e_1, e_2,..,e_a とすると、 e_1 に塗られていた色を e_2 に、e_2 に塗られていた色を e_3 に、 ...、 e_{a-1} に塗られていた色を e_a に、e_a に塗られていた色を e_1 に、同時に塗り替えることが出来ます。
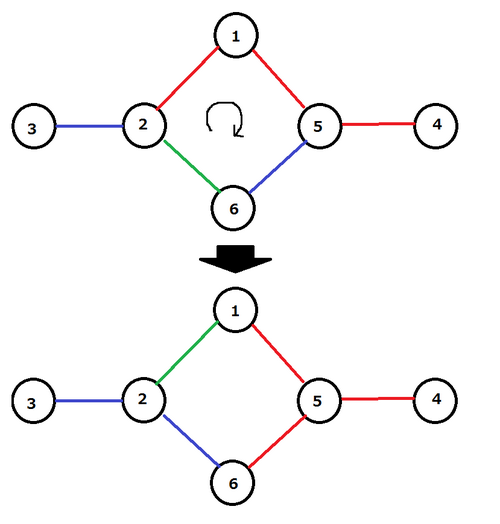
図1: 操作の例
塗り方Aと塗り方Bは、この操作を有限回行ってAからBに変形できるときに同じ塗り方だとみなします。グラフの塗り方が何通りあるか求めてください。ただしこの数は非常に大きくなることがあるので、 10^9+7 で割ったあまりを出力してください。
制約
- 1≦N≦50
- 1≦M≦100
- 1≦K≦100
- 1≦a_i,b_i≦N (1≦i≦M)
- グラフには自己ループや多重辺はない。
入力
入力は以下の形式で標準入力から与えられる。
N M K a_1 b_1 a_2 b_2 : a_M b_M
出力
塗り方が何通りあるかを 10^9+7 で割ったあまりを出力せよ。
入力例 1
4 4 2 1 2 2 3 3 1 3 4
出力例 1
8
入力例 2
5 2 3 1 2 4 5
出力例 2
9
入力例 3
11 12 48 3 1 8 2 4 9 5 4 1 6 2 9 8 3 10 8 4 10 8 6 11 7 1 8
出力例 3
569519295
Score : 1300 points
Problem Statement
One day, AtCoDeer the deer found a simple graph (that is, a graph without self-loops and multiple edges) with N vertices and M edges, and brought it home. The vertices are numbered 1 through N and mutually distinguishable, and the edges are represented by (a_i,b_i) (1≦i≦M).
He is painting each edge in the graph in one of the K colors of his paint cans. As he has enough supply of paint, the same color can be used to paint more than one edge.
The graph is made of a special material, and has a strange property. He can choose a simple cycle (that is, a cycle with no repeated vertex), and perform a circular shift of the colors along the chosen cycle. More formally, let e_1, e_2, ..., e_a be the edges along a cycle in order, then he can perform the following simultaneously: paint e_2 in the current color of e_1, paint e_3 in the current color of e_2, ..., paint e_a in the current color of e_{a-1}, and paint e_1 in the current color of e_{a}.

Figure 1: An example of a circular shift
Two ways to paint the edges, A and B, are considered the same if A can be transformed into B by performing a finite number of circular shifts. Find the number of ways to paint the edges. Since this number can be extremely large, print the answer modulo 10^9+7.
Constraints
- 1≦N≦50
- 1≦M≦100
- 1≦K≦100
- 1≦a_i,b_i≦N (1≦i≦M)
- The graph has neither self-loops nor multiple edges.
Input
The input is given from Standard Input in the following format:
N M K a_1 b_1 a_2 b_2 : a_M b_M
Output
Print the number of ways to paint the edges, modulo 10^9+7.
Sample Input 1
4 4 2 1 2 2 3 3 1 3 4
Sample Output 1
8
Sample Input 2
5 2 3 1 2 4 5
Sample Output 2
9
Sample Input 3
11 12 48 3 1 8 2 4 9 5 4 1 6 2 9 8 3 10 8 4 10 8 6 11 7 1 8
Sample Output 3
569519295